Developing tools to uncover the collective dynamics hidden within noisy brain activity patterns
Closing remarks for the NSF CAREER award IIS-1845836
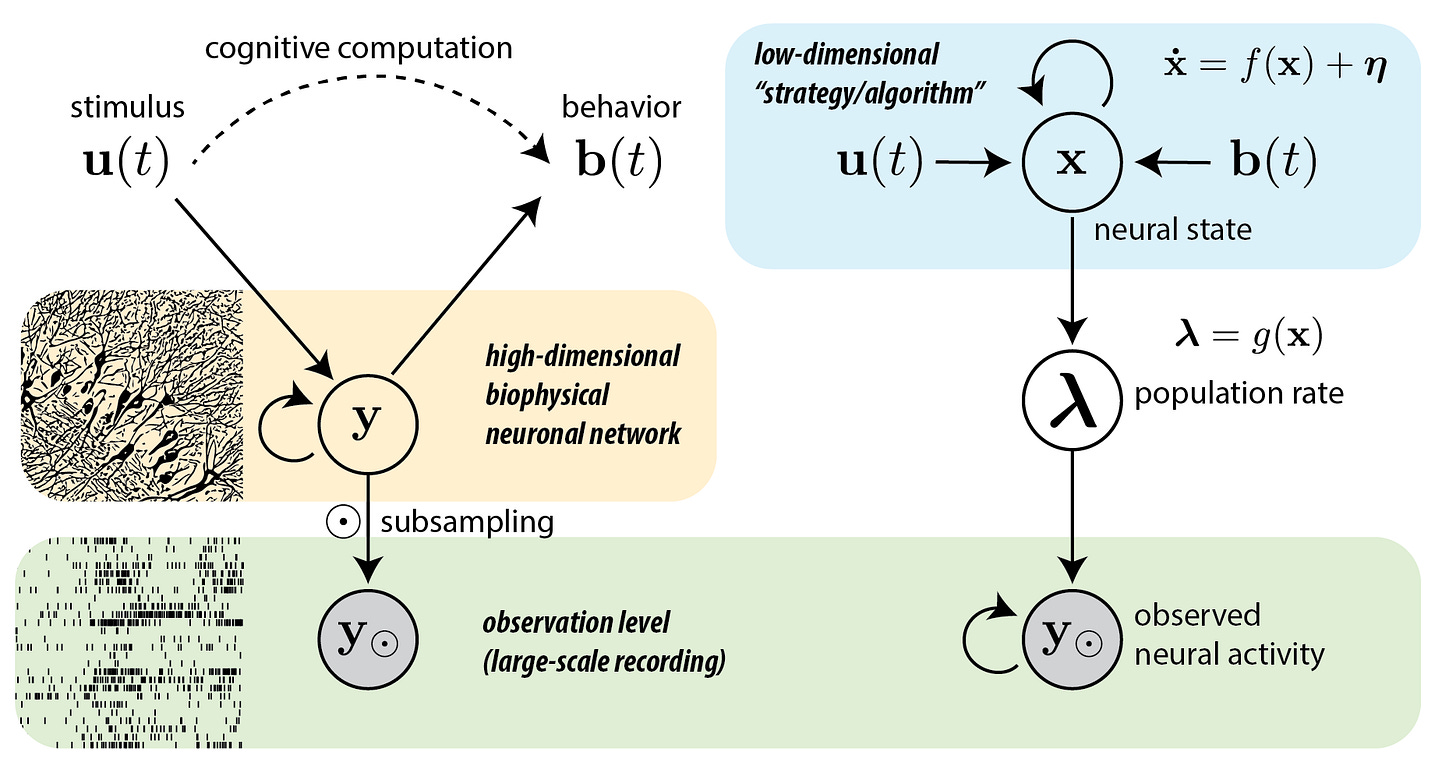
In 2018, when I was a tenure-track assistant professor at the Stony Brook University, I submitted an ambitious research grant proposal to the National Science Foundation (NSF) to uncover the “algorithm” underlying brain activity (related to the cognitive algorithms) and to access them in real-time. Unlike previous theoretical approaches that starts from mathematical principles, my approach was to let the measured neural activity tell us what the underlying algorithm was in the language of nonlinear dynamical systems. I called this data-centric inference the bottom-up approach. Despite the measurements being partial (only a fraction of the neurons involved in a large network computation), I assumed that the large-enough population activity could reflect the effective collective dynamics.
My proposal titled “CAREER: Dynamical Systems Modeling of Large-Scale Neural Signals Underlying Cognition” was awarded in the fall of 2019. The proposed research advanced mathmatical and statistical neurotechnology. It has concluded in 2023 after 4 years of research efforts.
There were three Aims of the research. Numbers in the parenthesis corresponds to the publications listed below.
Aim 1: Interpretable modeling of neural time series [1,2,3,4,6,7,8,11,15]
Interpretability of statistical model requires confident estimation, predictions and concise, causally interpretable explanations. We made several theoretical and practical advances for interpretable modeling of temporal processes. The first theoretical key result we showed was that in addition to the continuous attractors that are widely implicated, periodic and quasi-periodic attractors can also support learning arbitrarily long temporal relationships [Park et al. 2023a; Sokol et al. 2020]. We showed the advantage of nonlinear oscillations that are ubiquitos in the nervous system at various scales in training artificial recurrent neural networks, a result of interest on its own in the bourgeoning field of neuro-AI. The second is that the widely used Gaussian processes prior on neural trajectories is equivalent to a latent linear stochastic process through the Hida-Matern connection [Dowling et al. 2021]. This severely limits their ability to mimic nonlinear attractor dynamics and hence not appropriate for non-periodic long-term forecasting nor causal explanation. We also developed practical statistical neuroscience methods for estimating time constants in spontaneous dynamics [Neophytou et al. 2022], and improvements to the widely used autoregressive generalized linear models [Arribas et al. 2020; Dowling et al. 2020]. We showed that the lateralization in the recurrent connectivity in auditory cortex co-occurs with the longer network time constant measured during inter-trial intervals [Neophytou et al. 2022].
Aim 2: Real-time model fitting [9,10,12,13,14]
To unlock next-generation experiments where the neural state-space is perturbed and congtrolled in real-time (see Aim 3), we focused on speeding up the inference for streaming source of neural recording. Using the Hida-Matern connection, we developed a linear time inference for gaussian processes latent trajectory models [Dowling et al. 2023a]. We also improved previous online approximate Bayesian filtering methods by realizing that practically all methods assume an exponential family form of approximate posterior distribution [Dowling et al. 2023b, 2023c]. Those advances have greatly increased the quality and speed of inference.
Aim 3: Control algorithm for exploration of brain states [5]
The goal of this aim is to learn neural dynamics of disease attractor dynamics, and develop novel methods to explore the brain states in search for meta-stable states that can better support normal functions. We built a test platform, an analog electronic circuit, that exhibits bistable dynamics with a non-trivial unknown control policy [Jordan and Park 2020]. We have also developed and tested a novel control algorithm that maximizes exploration (manuscript in preparation). Our goal was to test the closed-loop system in traumatic brain injury patients in coma. Unfortunately, due to unforeseen issues that arose from the proposed collaboration, we were not able to make much progress on the planned human/animal studies. I plan to continue this line of research through RyvivyR and new collaborators.
So far, my lab generated a number of manuscripts with the support of this project (there are a few more cooking).
Sokół, P., & Park, I. M. (2020). Information geometry of orthogonal initializations and training. International Conference on Learning Representations (ICLR).
Dowling, M., Zhao, Y., & Park, I. M. (2020). Non-parametric generalized linear model. In arXiv [stat.ML]. arXiv. (revising)
Nassar, J., Sokol, P. A., Chung, S., Harris, K. D., & Park, I. M. (2020). On 1/n neural representation and robustness. Advances in Neural Information Processing Systems (NeurIPS).
Arribas, D. M., Zhao, Y., & Park, I. M. (2020). Rescuing neural spike train models from bad MLE. Advances in Neural Information Processing (NeurIPS).
Jordan, I. D., & Park, I. M. (2020). Birhythmic Analog Circuit Maze: A Nonlinear Neurostimulation Testbed. Entropy , 22(5), 537.
Dowling, M., Sokół, P., & Park, I. M. (2021). Hida-Matérn Kernel. In arXiv [stat.ML]. arXiv. (revising)
Jordan, I. D., Sokół, P. A., & Park, I. M. (2021). Gated Recurrent Units Viewed Through the Lens of Continuous Time Dynamical Systems. Frontiers in Computational Neuroscience, 15, 67.
Neophytou, D., Arribas, D. M., Arora, T., Levy, R. B., Park, I. M., & Oviedo, H. V. (2022). Differences in temporal processing speeds between the right and left auditory cortex reflect the strength of recurrent synaptic connectivity. PLoS Biology, 20(10), e3001803.
Dowling, M., Zhao, Y., & Park, I. M. (2023). Real-time variational method for learning neural trajectory and its dynamics. International Conference on Learning Representations (ICLR).
Dowling, M., Zhao, Y., & Park, I. M. (2023). Linear Time GPs for Inferring Latent Trajectories from Neural Spike Trains. International Conference on Machine Learning (ICML).
Park, I. M., Ságodi, Á., & Sokół, P. A. (2023). Persistent learning signals and working memory without continuous attractors. In arXiv [q-bio.NC]. arXiv. (revising)
Park, I. M. (2023). Fisher information of log-linear Poisson latent processes. (under review)
Dowling, M., Zhao, Y., & Park, I. M. (2023). Smoothing for exponential family dynamical systems. (under review)
Vermani, A., Park, I. M., Nassar, J. (2023). Leveraging generative models for unsupervised alignment of neural time series data. (under review).
Ságodi, Á., & Sokół, P. A., Park, I. M. (2023). RNNs with gracefully degrading continuous attractors. (under review)
Nassar, J. (2022) Bayesian Machine Learning for Analyzing and Controlling Neural Populations. PhD dissertation
Jordan, I. (2022). Metastable Dynamics Underlying Neural Computation. PhD dissertation
Sokół, P. (2023) Geometry of learning and representation in neural networks. PhD dissertation
Dowling, M. (2023). Approximate Bayesian Inference for State-space Models of Neural Dynamics. PhD dissertation