Bringing back Continuous Attractors
Perfect mathematical objects and their shadows in the brain
We have a new preprint that revives the theory of continous attractors that may be surprising to you! Despite their mathematical fragility, we show that they are functionally *robust*. No wonder we see approximate continuous attractors in neuroscience often. http://arxiv.org/abs/2408.00109
Ságodi, Á., Martín-Sánchez, G., Sokół, P., & Park, I. M. (2024). Back to the Continuous Attractor. arXiv. 2408.00109 (previous version is under review)
Dynamical systems theory teaches us to distinguish different topologies of flow (stability structures). One fixed point is totally different from two fixed points. These topological differences determine their asymptotic behavior, which can be qualitatively described in discrete categories.
If changing a parameter of the system causes the topology of the flow to change, it is a big deal. This is the study of bifurcations.
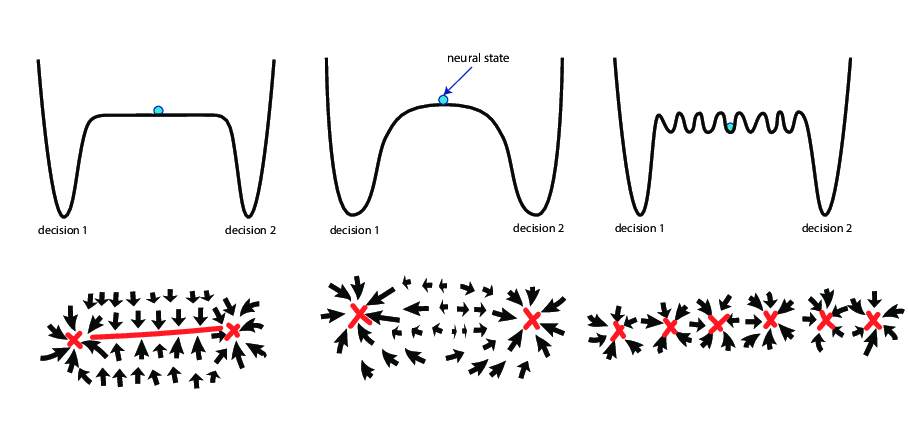
Continuous attractors are widely used in theoretical and computational neuroscience. They are special topological structures where there is an attracting manifold of fixed points. They are hypothesized and sought after whenever there is a continuous variable, such as head direction, location, or intensity, that needs to have a persistent internal representation.
However, they are so special that in the space of dynamical systems, they are super rare. (Image by DALL-E & ChatGPT) That makes them fragile, since almost any perturbation to their flow destroys them.
In biological neural systems, the synaptic weights are constantly fluctuating and stochaticity in learning rules continously introduces variations in the parameters of the recurrent dynamics. In artifical recurrent neural networks, we often train them with stochastic gradients and numerical errors influences their parameters. Across animals and initial conditions, there are variations in their solutions as well. This means general continuous attractors that require fine-tuning cannot exist in the wild (if they existed by some miracle, they will be destroyed very soon).
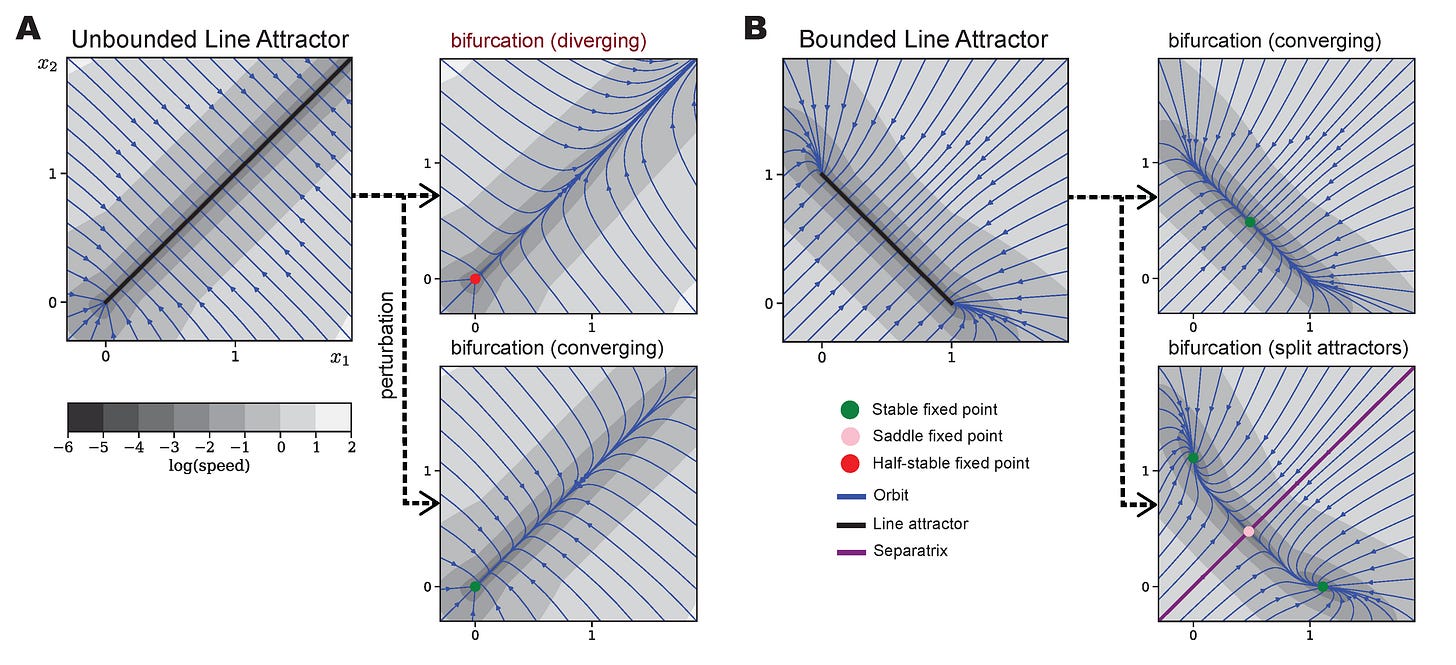
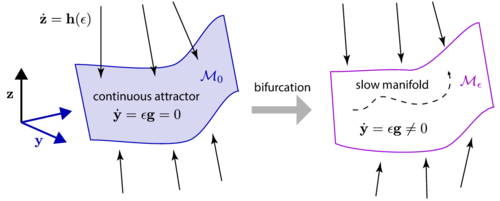
However, continuous attractors with a mild condition do not completely vanish when they are destroyed. They leave a ghost of their existence. A shadow. A **slow manifold**.
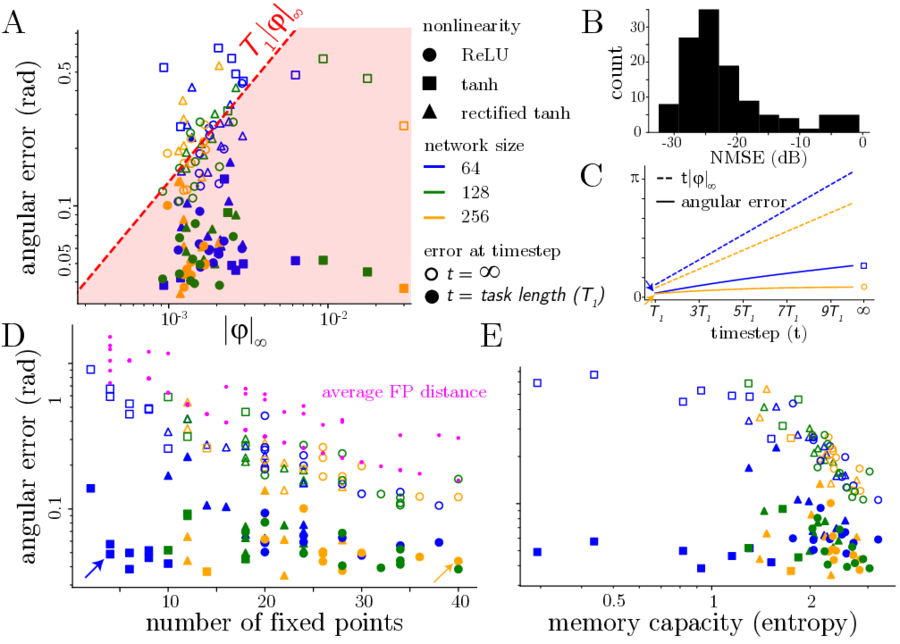
The mild condition is that the attraction to the manifold being fast enough in all directions (called “normal hyperbolicity”). Our theory guaranetees their short-term behavior to be close to the continuous attractor given a small perturbation in their flow.
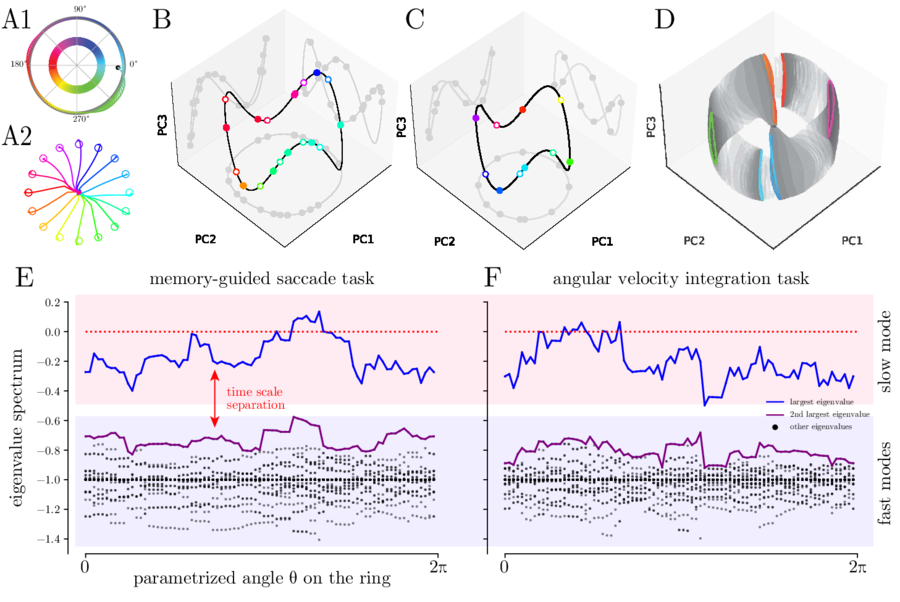
We also trained RNNs to perform tasks that require continous memory and found approximate ring attractors. Due to the noise injected to the internal state, and the stochastic gradient descent training, the solutions exhibit normal hyperbolicity (panel E below). Therefore, the RNNs can be shown to be near to the mathematically perfect continuous attractor.
Our theory is quite general. It works for any parameterization of the dynamics as long as the network is flexible enough to bifurcate away from the continuous attractor. It works for higher dimensional manifolds, although we only empirically tested up to 2D.
Like the Platonic "idea", the continuous attractor is useful since nearby objects are approximately continuous attractors. So, if you were scared due to the fine-tuning problem, I hope we convinced you that they are much less fragile than once thought.
Many examples, derivations, and proper citations are in the paper. If you are intrigued, give it a go!